- Услуги
- Цена и срок
- О компании
- Контакты
- Способы оплаты
- Гарантии
- Отзывы
- Вакансии
- Блог
- Справочник
- Заказать консультацию
Заказать консультацию
Основы теории экстремальных значений
Дана последовательность независимых одинаково распределенных случайных величин: η1, η2…., ηn…. с функцией распределения F(x).
Можно рассмотреть новую последовательность случайных величин {Mn}, где Mn = max {η1, η2…., ηn….}, n = 1, 2, 3…..
Функция распределения случайной величины Mn определяется следующим образом:

Теорема Фишера-Типпета
Дана последовательность независимых одинаково распределенных случайных величин η1, η2…., ηn…..


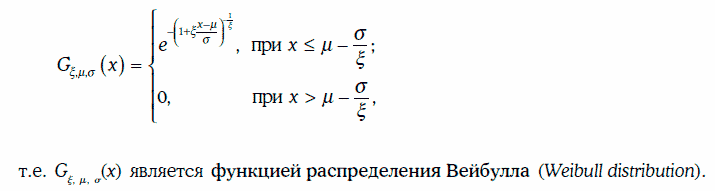
Следствие из теоремы Фишера – Типпета
Если случайные величины η1, η2, …, ηn независимы и одинаково распределены, а n достаточно велико, то функция распределения случайной величины Mn = max{η1, η2, …, ηn} практически совпадает с функцией обобщенного распределения экстремальных значений (при подходящем выборе параметров ξ, μ и σ).
Предположим, что случайная величина Mn = max{η1, η2, …, ηn} имеет распределение Фреше, т. е.
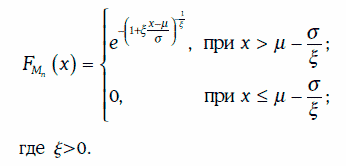
Тогда справедливы следующие утверждения:
1. Плотность распределения случайной величины Mn имеет следующий вид (рис. 1).
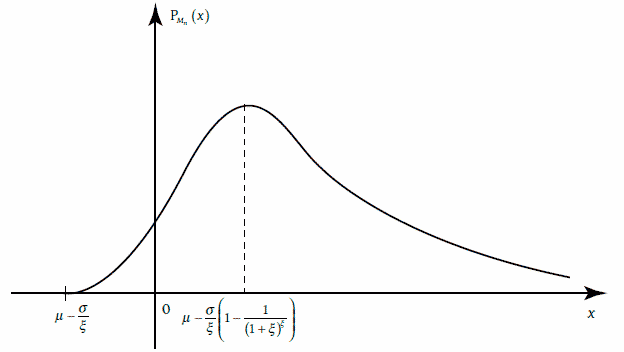
Рис. 1. График функции плотности распределения Фреше
2. Математическое ожидание и дисперсии случайной величины Mn можно найти по формулам:
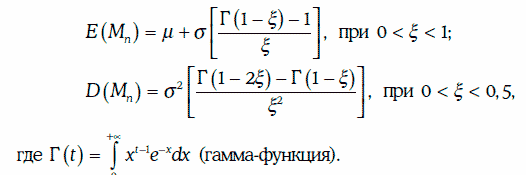
Параметры ξ, μ, σ можно подобрать на основе статистических данных.
Для измерений экстремальных событий может быть использовано распределение Парето (Pareto distribution), которое определяется функцией:
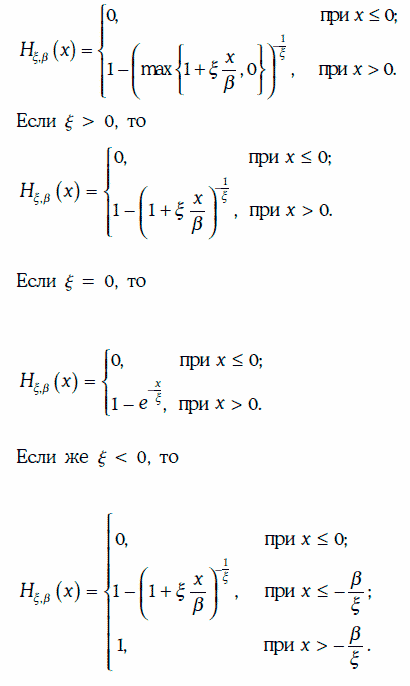
Для большого класса случайных величин η при достаточно большом пороговом значении u справедливо равенство:
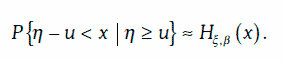
Данное соотношение позволяет оценивать «хвосты» распределений на основе статистических данных.
Статьи по теме
- Краткий обзор Нового базельского соглашения по капиталу
- Модель управления активами и пассивами (ALM)
- Метод сигналов
- Подход на основе регрессионного анализа
- Модели возникновения финансовых кризисов
- Минимальные требования к достаточности капитала с учетом кредитного и рыночного рисков
- Подход на основе внутренних моделей банков. Верификация моделей расчета VaR по историческим данным
- Подход на основе внутренних моделей банков. Количественные критерии
- Подход на основе внутренних моделей банков. Качественные критерии
Полезные статьи









Узнайте цену услуг:
Узнай цену консультации
"Да забей ты на эти
дипломы и экзамены!”
(дворник Кузьмич)

